[paper_reading]-"Visual Odometry Part I&II"

Posted on   |   Updated on | In | 本文总阅读量 次
Words count in article: 4.5k 字 | Reading time ≈ 17 分钟

1. Overview of VO

　　SFM(Structure from Motion) 是解决从一堆图片中将场景以及相机姿态进行 3-D 重建的问题，最后的场景以及相机姿态可以通过离线优化方法（bundle adjustment）来 refine。VO & VSLAM 都属于 SFM 的特殊情况，SfM 处理的图像时间上可以是无序的，而 VO & VSLAM 则要求图像时间上有序。VO 只关心轨迹的局部一致性，而 VSLAM 关心全局轨迹和地图的一致性。VO 可以作为 VSLAM 的一个模块，用于重建相机的增量运动，Bundle Adjustment 可以用来 refine 相机的轨迹。如果用户只对相机路径感兴趣，不需要环境地图，且需要较高的实时性，那么一般 VO 就能满足需求。
　　视觉里程计（VO）最早应用于 NASA 火星地面探测器，相比于车轮里程计的优势：

  • 不受车轮打滑的影响；
  • 不受拐弯影响，拐弯时左右轮速度不一样；
  • 更加准确，相对位置误差大概在 0.1% 到 2%，可作为车轮里程计、GPS，IMU等其它测量装置的补充；
  • 在某些领域是必须的，比如无法使用车轮里程计的无人机，GPS 失效的水下环境等；

　　根据视觉传感器数量，VO 可分为 Stereo VO，与 Monocular VO。当场景距离远远大于双目基线时，Stereo VO 也需要退化成 Monocular VO 来处理。

1.1. Stereo VO & Monocular VO

　　特征点匹配可以通过特征跟踪（Feature Tracking）或特征检测（Feature Detect）再匹配两种方式实现。特征跟踪计算量小，但是容易漂移；特征检测再匹配计算量大，需要用 RANSAC 去除无匹配点，但是特征点不容易漂移。
　　Motion Estimation 可通过 3D-3D，3D-2D，2D-2D 三种方式实现。Stereo 系统可以获得每个点的深度信息，所以这三种方式都可以用来做相机的运动估计。实验表明，直接在原始的 2-D 点上进行相机运动的估计，更加准确（？存疑）。
　　之所以研究单目 VO，是因为当场景距离相机很远的时候（相对于双目的基线），双目就退化为单目了。单目 VO 中绝对深度（尺度）是未知的，刚开始两帧相机移动的距离通常设定为 1，之后的相对位姿都基于此。相关方法可分为：

  • Feature-based Methods，用每一帧的特征点来估计运动。
  • Appearance-based Methods，用图像中所有的像素点或是子区域中的像素点来估计运动。
  • Hybrid Methods，结合以上两种形式。

第一种方法较好，运动估计用 five-point RANSAC 来求解。

1.2. Reducing the Drift

　　由于 VO 是一步步计算相机的运动轨迹然后作累加的，那么误差就有累积性，使得估计的运动轨迹会漂移。这可以用 Sliding Window(Windowed) Bundle Adjustment 局部优化方法来解决。也可以用 GPS 或 laser 或 IMU 融合来解决。Windowed Bundle Adjustment，是通过 m 个窗口下的信息来优化求解这 m 个相机位姿。

1.3. VO Versus V-SLAM

　　V-SLAM 两大方法：

  • Filtering Methods 概率法，以一定的概率分布融合所有图像信息；
  • Keyframe Methods 关键帧法，使用全局 Bundle Adjustment 优化被选择的关键帧；

　　VO 只关心相机轨迹的一致性，而 SLAM 关注轨迹与地图整体的一致性。SLAM 中两大问题是，检测 loop closure 的发生以及用这个约束来更好的优化当下的地图和轨迹。而 VO 只对历史中以往 n 个轨迹中的位姿进行优化（windowed bundle adjustment），这可以认为与 SLAM 中建立局部地图与轨迹是等价的。但是这两者的 philosophy 不同：

  • VO 只关心局部轨迹的一致性，局部地图只是用来（在 bundle ajustment）更精确的估计局部轨迹；
  • SLAM 关心整个地图的一致性，当然也包括轨迹，轨迹的精确性能使地图更加精确；

　　VO 可以是 SLAM 的一个模块（相机运动轨迹的重建），SLAM 还需要一个闭环检测，以及一个全局的地图优化策略。V-SLAM 重建相机运动轨迹理论上比 VO 更精确（加入了更多的约束），但是不一定更鲁棒，因为闭环检测中的奇异值对地图的一致性有较大影响。此外 SLAM 更加复杂以及耗计算资源。VO 牺牲了全局一致性，来达到实时运行的目的，因为不需要记录所有的地图信息。

2. Formulation of the VO Problem

　　在时间 \(k\) 下，相机拍摄的图像集记为：\(I_{0:n}=\{I_0,...,I_k\}\)。相机在时间 \(k-1\) 与 \(k\) 的位姿转换矩阵为 \(T_{k,k-1}\in \mathbb{R}^{4\times 4}\)。VO 所要求解的问题就是 \(T=T_{1,0}T_{2,1}...T_{k,k-1}\)。由此可知 VO 是计算相邻帧的相机位姿，然后对之前 m 个位姿做一个局部优化从而估计更准确的轨迹。 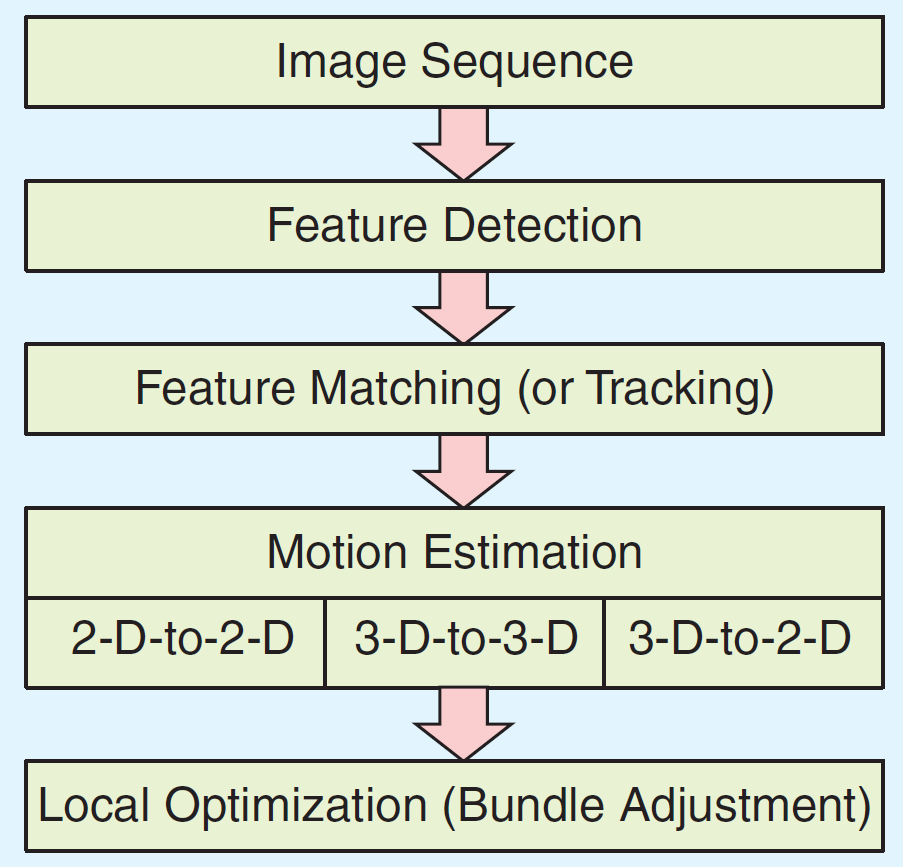　　大多数 VO 算法是基于特征点来估计运动的，特征点法的流程如图 1. 所示：

  1. Feature Detection(Extraction) and Matching/Feature Tracking
    特征提取并与上一帧的特征进行匹配，或者直接用上一帧的特征在这一帧进行跟踪；
  2. Motion Estimation
    在 \(k,k-1\) 帧之间求解 \(T_{k,k-1}\) 的过程，根据匹配的特征点对是 2D 还是 3D，运动估计可分为 3D-3D，3D-2D，2D-2D 三种方式实现；
  3. Local Optimization
    在 \(k,k-m\) 帧用 Bundle Adjustment 迭代优化求解最优的局部轨迹；

本文会重点阐述 Camera Model[1]，Feature Detection and Matching[2]，Motion Estimation[1]，Robust Estimation[2]，Local Optimization[2]。

3. Camera Modeling and Calibration

　　相机模型及标定，另文详述。

4. Feature Detection and Matching/Feature Tracking

　　生成前后帧特征点的匹配对，有两种方法：

  • feature tracking
    用局部搜索的方法，较适用于相邻两帧视角变化不大的情况，会有漂移（drift）的现象；
  • feature detection and matching
    独立在每个图像上进行检测，然后用某种度量准则进行匹配。在视野变化较大的情况下，只能用这种方法；

4.1. Feature Tracking

　　主要采用 KLT（详见 KLT 算法详解）方法进行特征点跟踪。

4.2. Feature Detection and Matching

　　特征点包含特征检测子与特征描述子。一个好的特征点应该有如下性质：

  • 可重复性(Repeatability)，不同图像下相同特征点可再次检测出；
  • 可区别性(Distinctiveness)，不同特征点表达形式不一样，可以更好匹配；
  • 高效率(Efficiency)，计算高效；
  • 本地性(Locality)，特征仅与一小片图像区域有关；
  • 定位准确(Localization Accuracy)，不同尺度下定位都要准确；
  • 鲁棒性(Robustness)，对噪声，模糊，压缩有较好的鲁棒；
  • 不变性(Invariance)，对光照(photometric)，旋转，尺度，投影畸变(geometric)有不变性；

4.2.1. Feature Detector

　　特征检测子（feature detector）的计算过程包含两步，首先将图像进行一个特征响应函数的变换，比如 Harris 中的 角点响应函数，SIFT 中的 DoG 变换；然后应用非极大值抑制，提取最小或最大值。
　　特征检测子可分为两类：

  • 角点(corners)
    角点检测子被定义为至少两个边缘相交的地方；角点计算快，定位精度高，但是区分度低，大尺度下定位精度低；
  • 斑点(blobs)
    斑点检测子被定义为一种与周围区域在亮度、颜色、纹理下不同的模式；区分度较高，但是速度较慢；

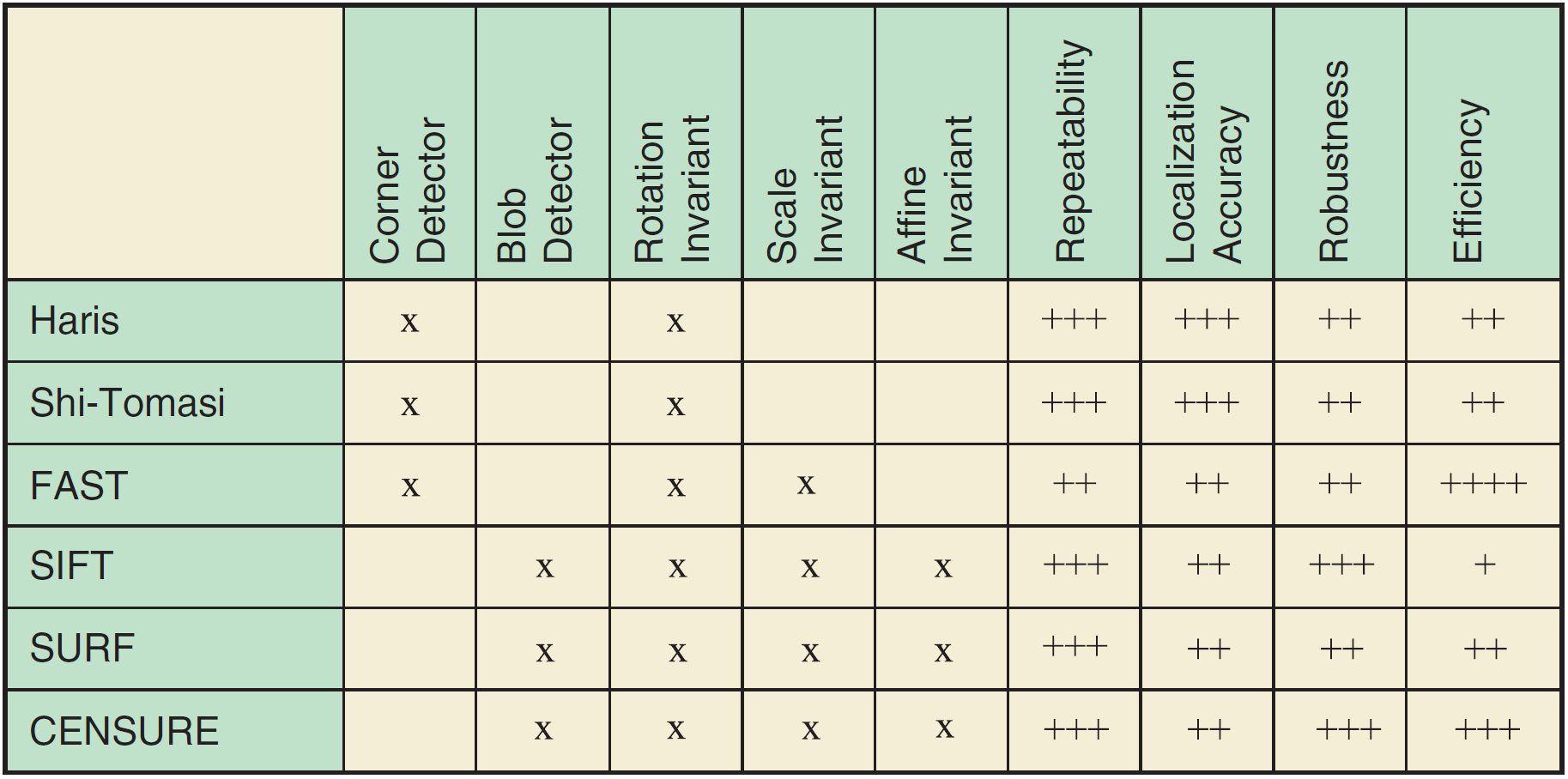　　如图2. 所示，常用的角点检测子有 ORB 特征中的 FAST 关键点，Harris 角点等；常用的斑点检测子有 SIFT，SURF，CENSURE 等。

4.2.2. Feature Descriptor

　　有了特征检测子后，为了特征点匹配，还需要描述这个检测子，描述量称为特征描述子。描述子可分为以下几类：

  1. Appearance，检测子周围的像素信息
    • SSD 匹配，sum of squared difference，计算检测子周围像素亮度与其的误差和；
    • NCC 匹配，normalized cross correlation，相比 SSD，有一定的光照不变性；
    • Census Transform，将检测子周围的 patch 像素与其进行对比，合成 0,1 向量；
  2. Histogram of Local Gradient Orientations
    • SIFT，光照，旋转，尺度，均具有不变性；不适用于角点，适用于斑点；
  3. Much Faster
    • BRIEF，二进制描述子，用于 ORB；对于旋转和尺度有较强的区分性，并且提取以及比较速度都很快；

　　目前常用的 ORB 特征，采用的是 Oriented FAST 角点，以及 BRIEF 描述子。

4.2.3. Feature Matching

　　通过比较特征点中的描述子部分，来完成特征点的匹配。如果是 appearance 描述子，那么一般通过 SSD/NNC 来计算描述子之间的相似度，其它二进制描述子，可通过欧氏距离或汉明距离来度量。
　　基于相似性度量的特征匹配，最简单的就是暴力匹配，两组特征点挨个计算相似度。暴力匹配时间复杂度较高，通常我们采用快速近似最近邻算法（FLANN），也可以加入运动估计模型（通过 IMU 等装置获得的大致运动位姿）来缩小搜索范围。特殊的如果是双目系统，因为左右目图像都是矫正过的，所以左右目的特征点匹配可通过行矩阵搜索解决。
　　匹配结束后，我们还得进一步验证匹配的正确性，去除误匹配的情况。比如相互一致性验证，每个特征点只能匹配一个特征点。
　　实验表明特征点的分布也很影响匹配效果，特征应尽量均匀分布，可以将图像栅格化，然后对不同的栅格用不同的特征检测阈值即可，保证栅格之间特征数量相等。

5. Motion Estimation

5.1. 2D-2D

　　这种情况下特征点 \(f_{k-1},f_k\) 分别是在 2D 图像 \(I_{k-1},I_k\) 坐标系上。
　　对极约束推倒过程可详见这里。根据对极约束，可推导出同一 3D 点投影到两个相机视角图像下后，其坐标之间的关系： \[p_2^TK^{-T}t^{\wedge} RK^{-1}p_1=0\] 记本质矩阵(Essential Matrix)\(E=t^{\land} R\)，记基础矩阵(Fundamental Matrix)\(F=K^ {-T}EK^ {-1}\)。基础矩阵描述的是两幅图像对应点的像素坐标的关系；本质矩阵描述的是世界中的某点分别在两个相机坐标系下坐标的相对关系。
　　一般相机内参是已知的，所以我们求解本质矩阵。可采用五点法或者八点法来求解，五点法只能处理已知相机标定参数的情况，所以我们一般采用八点法来求解本质矩阵 \(E\)，大于八点即可用最小二乘求解线性方程。然后对本质矩阵进行奇异值分解，即可求出相机的位姿 \(R,t\)。
　　当选取的点共面时，基础矩阵的自由度下降，即出现退化的现象，这个时候需要同时求解单应矩阵\(H\)，选择重投影误差较小的那个作为最终的运动估计矩阵。
　　此外，还需计算当前运动的相对尺度，可由 3D 点的位置信息求解相对尺度。绝对尺度的求解需要三角化求解。
　　总结过程如下：

  1. 得到新的当前帧 \(I_K\);
  2. 提取当前帧的特征点，并与上一帧的特征进行匹配；
  3. 根据匹配的特征点对，计算本质矩阵\(E\)；
  4. 奇异值分解本质矩阵，得到相机运动 \(R_K,t_k\)；
  5. 该相邻帧的相机运动信息与之前相机运动信息进行累计；
  6. 重复 1.；

5.2. 3D-2D

　　这种情况下，特征点 \(f_{k-1}\) 是 3D 坐标点，\(f_k\) 是其投影到 2D 图像 \(I_K\) 上的匹配点。对于单目的情况，\(f_{k-1}\) 需要从相邻的前面帧中（比如 \(I_{k-2},I_{k-1}\)）三角化出 3D 坐标，然后与当前帧进行匹配，至少需要三帧的视角。3D-2D 比 3D-3D 更加精确，因为 3D-3D 直接优化相机运动，没有优化投影的过程。
　　该问题也称为 PnP(Perspective from n Points)。PnP 问题有很多种求解方法：

  • P3P 只是用 3 个点对进行求解，容易受误匹配的影响；
  • 直接线性变换 需要 6 对匹配点才能求解，如果大于 6 对，则可用 SVD 等方法求线性方程的最小二乘解；
  • EPnP
  • UPnP
  • 非线性优化(Bundle Adjustment)

记 \(p_{k-1}^ i\) 为 \(k-1\) 时刻下第 \(i\) 个特征点在相机坐标系下的坐标，定义重投影的误差项： \[\xi=\mathop{\arg\min}\limits_{T_{k,k-1}} \sum_i \left\Vert uv^i_k-K \, T_{k,k-1} \, p_{k-1}^i \right\Vert^2\]

　　总结过程如下：

  1. 初始化，在 \(I_{k-2},I_{k-1}\) 两张图里提取特征并匹配，三角花得到特征点的 3D 坐标；
  2. 在 \(I_k\) 图像中提取特征点，并与上一帧的特征进行匹配；
  3. 用 PnP 求解相机运动；
  4. 在 \(I_{k-1},I_{k}\) 中三角化所有特征点；
  5. 重复 2.；

5.3. 3D-3D

　　这种情况下特征点都是 3D 坐标点，都需要三角花得到，可以使用一个立体视觉系统。
　　已知两组匹配好的 3D 点，可以用 ICP(Iterative Closest Point) 来求解位姿。ICP 有两种求解方式：

  • 线性求解
  • 非线性优化(类似 Bundle Adjustment)

定义重投影的误差项： \[\xi=\mathop{\arg\min}\limits_{T_{k,k-1}} \sum_i \left\Vert p_{k}^i - T_{k,k-1} \, p_{k-1}^i \right\Vert^2\]

　　ICP 问题存在唯一解或无穷多解的情况，所以非线性优化时，只要找到极小值，那一定是全局最优解，这也意味着 ICP 非线性优化时可以任意选定初始值。
　　在匹配已知的情况下，ICP 问题是有解析解的。不过如果有些特征点观察不到深度，那么可以混合着使用 PnP 和 ICP 优化：对于深度已知的特征点，建模 3D-3D 误差，对于深度未知的特征点，建模 3D-2D 的重投影误差。两个误差项，用非线性优化求解。

5.4. Triangulation and Keyframe Selection

　　对于 stereo camera， 3D-2D 比 3D-3D 更准确；3D-2D 比 2D-2D 计算更快，前者是 P3P 问题，后者则至少需要 5 个点。当场景中物体相比基线很大时，那么立体视觉系统就失效了，这时候用单目视觉系统比较靠谱。
　　对于 monocular camera，2D-2D 比 3D-2D 看样子更好，因为避免了三角测量；然后实际中，3D-2D 用得更多，因为数据关联更快。
　　当两帧之间相隔很短时间时，可以认为基线非常小，这种情况，获得的深度信息不确定性很高，所以需要选择某些 keyframes 来计算。

6. Robust Estimation/Outlier Rejection

　　匹配的特征点可能因为噪音、遮挡、模糊、视角变化、光照变化等原因成为外点（outliers），这时候该匹配对对运动估计来说就是个外点，估计的时候应该想办法去除掉。
　　RANSAC 目前已是在含有噪声的数据中进行模型估计的标准方法。其思想是随机选取一些数据进行建模，涵盖数据最多的模型即被选择是最终模型。对于相机运动估计来说，模型就是相机的运动 \(R,t\)，数据就是特征匹配对。RANSAC 流程为：

  1. 初始化，记 A 为特征点对集；
  2. 从 A 中随机选取一些点对 s；
  3. 用 s 估计运动模型；
  4. 计算所有的点对与这个模型的距离误差，可使用 point-to-epipolar 距离或是 directional 误差(Sampson distance)；
  5. 统计距离误差小于一定阈值的点对的数量，并存储标记这些内点(inliers)；
  6. 重复 2.，直到达到最大迭代次数；
  7. 选取数量最多的内点点对集，用这些点估计最终模型；

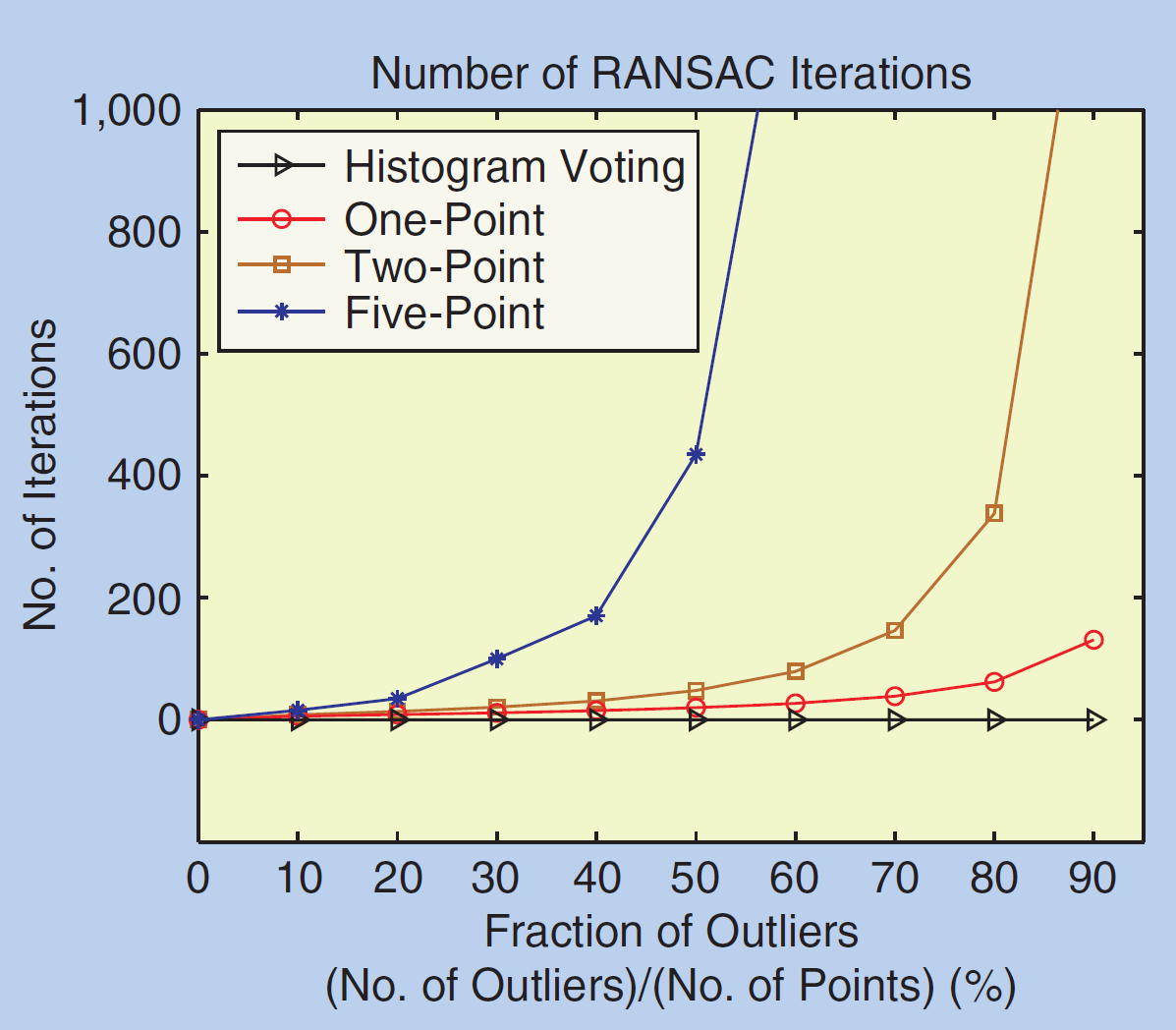
　　为保证得到正确解，迭代次数要求： \[N=\frac{log(1-p)}{log(1-(1-\epsilon)^s)}\] 其中，\(p\) 表示得到正确解的概率，\(\epsilon\) 表示外点的百分比，\(s\) 表示每次模型估计取出的点数。如图 3. 所示，选出的点数越少，迭代次数就可以越少。这个角度来讲，五点法比八点法有优势，但是五点法的前提是相机都是标定过的。不过不考虑速度的话，还是选择更多的点，因为可以平滑噪声。

7. Local Optimization

　　每次估计的相机运动都有误差，随着运动的累计，误差也会累计。这就要求做局部最优化，消除轨迹的漂移。优化方式有 Pose-Graph Optimization（需要回环检测） 以及 Windowed Bundle Adjustment 两种，这里主要介绍 BA。定义误差函数： \[\xi=\mathop{\arg\min}\limits_{X^i,C_k} \sum_{i,k} \left\Vert uv_{k}^i - g(X^i,C_k) \right\Vert^2\] 其中 \(X^i\) 为世界坐标系下特征点的 3D 坐标，\(C_k = T_{1,0}...T_{k,k-1}\)，\(g(X^i,C_k)\)为特征点投影到图像的映射函数。该非线性问题可用 Newton-Gauss 或 LM 法解决。为了加速运算，如果 3D 特征点是准确的(如立体视觉获得的)，那么可以固定特征点的 3D 量，只优化相机的轨迹。

[1] Scaramuzza, Davide, and Friedrich Fraundorfer. "Visual odometry [tutorial]." IEEE robotics & automation magazine 18.4 (2011): 80-92.
[2] Fraundorfer, Friedrich, and Davide Scaramuzza. "Visual odometry: Part ii: Matching, robustness, optimization, and applications." IEEE Robotics & Automation Magazine 19.2 (2012): 78-90.

----------------- END -----------------
坚持原创技术分享！